균형 이진 탐색 트리(AVL 트리)

본 내용은 Deep Into Algorithm from MIT 강의를 들으며 정리한 내용이다.

이전 포스팅에 다룬 이진 탐색 트리(BST)에서 이어지는 내용이다.

혹시 보지 않았거나 가물가물하다면 이전 포스팅을 한 번 보고 오는 것을 추천한다.

https://mrlee.kr/entry/%EC%9D%BC%EC%A0%95-%EC%98%88%EC%95%BD%EA%B3%BC-%EC%9D%B4%EC%A7%84-%ED%83%90%EC%83%89-%ED%8A%B8%EB%A6%ACBST?category=788297

일정 예약과 이진 탐색 트리(BST)

 

먼저, 이진 탐색 트리에서 높이란 "루트부터 단말 노드까지 가장 긴 하향 경로의 길이" 이다.

이전 포스팅에서 문제로 남았던 것이 바로 "균형"이다.

이진 탐색 트리는 삽입, 삭제, 최솟값, 최댓값 등을 O(h) 안에 실행할 수 있다.
이 때 h가 트리의 높이이며 (lg n < h < n) 범위를 가진다.

이진 탐색 트리 균형 맞추기

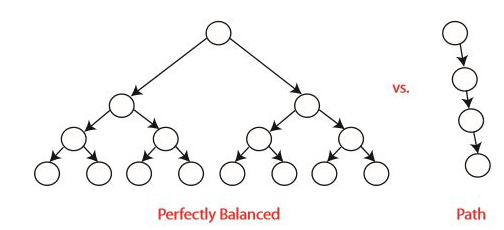
여기서 이진 탐색 트리가 균형이 잡히면 h = O(lg n)으로 유지된다.
→ 모든 작업을 O(lg n) 시간 안에 실행 가능하다.

바로 균형 이진 탐색 트리를 유지하기 위해 AVL 트리를 활용할 수 있다.

AVL 트리의 조건은 단순하다. 트리의 높이를 활용하는 것이다.
AVL 트리는 높이를 활용하기 위해 노드마다 자신의 높이를 저장한다.

• 모든 노드에 대해, 왼쪽과 오른쪽 자식들의 높이 차는 최대 ±1이다.
  • 각 노드마다 높이를 저장해야 한다.
  • 자식이 없는 단말 노드는 왼쪽, 오른쪽 각각 NULL pointer를 가진다.
  • NULL pointer는 -1의 높이를 가진다고 가정한다.

여기서 깊이와 높이를 혼동할 수 있기 때문에 주의해야 한다.
높이와 다르게 깊이는 단순히 노드의 단계(깊이)를 의미한다.

AVL 트리의 시간 복잡도를 살펴보자.

먼저 기본적인 전제를 활용할 것이다.

• 모든 AVL 트리는 균형을 이룬다.(트리의 높이가 lg n의 상수 배다.)

최악의 경우를 살펴보자. 최악의 경우는
모든 노드에서 오른쪽 서브 트리의 크기가 왼쪽 서브트리 높이보다 1만큼 큰 경우이다.

이때 노드가 n 개라면 최악의 경우 h = n이겠지만
우리는 $$h = 2^n$$ 을 이루는 것을 원하는 것이다.

이제 재귀식을 작성해보자.

$$T(1) = 1$$ $$T(2) = 2$$ $$T(h) = 1 + T(h-1) + T(h-2)$$

AVL 트리 개념

결국 AVL 트리는 위와 같은 그림처럼 구성되었기 때문에
탐색을 위해 왼쪽 자식 노드의 높이와 오른쪽 자식 노드의 높이에 부모 노드를 더한 재귀식이 성립한다.

$$T(h) = 1 + T(h-1) + T(h-2)$$ $$T(h) > 2T(h-2)$$ $$T(h) > 2^{h/2}$$ $$h > 2log(T(h))$$

여기서 

$$T(h) > 2^{h/2}$$

부분으로 넘어가는 과정이 혼동될 수 있는데 이 식은 수학적 귀납법으로 성립함을 증명할 수 있다.

1. h = 1, 2 일 때 성립한다.
2. h = k, k+1 일 때 성립한다고 하면 (k >= 1)

$$T(k+2) = 1+T(k+1)+T(k)>1+2^{(k+1)/2}+2^{k/2}>2*2^{k/2}= 2^{(k+2)/2}$$ 이므로 h = k + 2 일 때도 성립한다는 것을 증명할 수 있다.

 

따라서 트리의 높이가 O(lg n)으로 유지된다는 것을 확인할 수 있었다.

 

[AVL 삽입]

그렇다면 이제 AVL 트리에 어떻게 삽입하는지 알아보자.

AVL 삽입 알고리즘은 간단하다.

1. 간단한 이진 탐색 트리로 삽입
2. 트리를 따라 올라가면서 AVL 속성을 회복하도록 처리(올라가면서 높이값도 갱신)

이 갱신하는 과정이 생각보다 어렵다.

일단 아래와 같은 알고리즘으로 AVL 속성을 회복할 수 있다.

• x가 AVL을 위반하는 가장 낮은 노드라고 가정
• x가 오른쪽-무거움(오른쪽 자식 노드가 더 높다.)이라고 가정(왼쪽은 대칭임)
• if x의 오른쪽 자식이 오른쪽-무거움이나 균형이라면 Left-Rotation(x) 수행
• else Right-Rotation(x의 자식 노드) 수행 후 Left-Rotation(x) 수행
• x의 조부모, 증조부모 노드로.. 루트까지 올라가며 계속함

만약 x가 왼쪽-무거움이라면 Left-Rotation, Right-Rotation만 반대로 진행해주면 된다.

Rotation을 균형이 무너진 유형 4가지를 살펴보며 알아보자.

LL

왼쪽 높이가 2인데 오른쪽은 -1(NULL)인 경우이다. 이 경우 Right-Rotation을 해주면 된다.

Right-Rotation이란 쉽게 생각하면 우회전이다.
마치 위에서부터 노드들이 오른쪽으로 한 칸씩 이동한 것처럼 보이게 움직여주면 된다.

구체적인 코드로 구현할 때는
가장 위의 노드(20)를 두 번째 노드(18)의 오른쪽 자식으로 넣어주면 된다.

RR

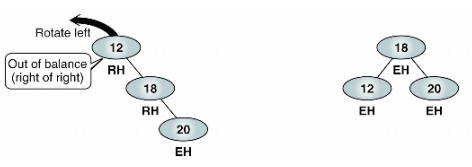
왼쪽 높이가 -1인데 오른쪽은 2인 경우이다. 이 경우 Left-Rotation을 해주면 된다.

Right-Rotation이란 쉽게 생각하면 좌회전이다.
마치 위에서부터 노드들이 왼쪽으로 한 칸씩 이동한 것처럼 보이게 움직여주면 된다.

구체적인 코드로 구현할 때는
가장 위의 노드(12)를 두 번째 노드(18)의 왼쪽 자식으로 넣어주면 된다.

RL

왼쪽 높이가 2이며 오른쪽은 0인 경우인데 LL과는 살짝 다르다. 왼쪽 서브 트리의 모양이 '<' 이렇게 생겼다.

이 때는 두 번째 노드를 Left-Rotation 한 후에 전체 노드를 기준으로 Right-Rotation 한 번 해주면 된다.

LR

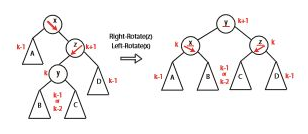
왼쪽 높이가 0이며 오른쪽은 0인 경우이다. RR과는 살짝 다르다. 왼쪽 서브트리의 모양이 '>' 이렇게 생겼다.

이 때는 두 번째 노드를 Right-Rotation 한 후에 전체 노드를 기준으로 Left-Rotation 한 번 해주면 된다.

 

이와 같은 방법으로 이진트리의 균형을 유지하며 데이터 삽입을 할 수 있다.

일반적으로 삽입을 위해 여러 번의 회전이 필요하다.
삭제도 조금 더 어렵겠지만 이와 같은 방법으로 구현이 가능하다.

그렇다면 AVL 트리를 또 어떻게 활용할 수 있을까?

정렬에도 활용할 수 있다.

단순히 AVL 트리에 모든 데이터를 넣은 후 중위 순회로 탐색하면 정렬된 순서로 읽어올 수 있다.

그래서 AVL트리를 활용한 정렬은 아래와 같은 시간이 소요된다.

• AVL 트리에 각 아이템 삽입 → Θ(nlg n)
• 중위 순회  → Θ(n)/ Θ(nlg n)